Torsi
Torsi atau momen gaya adalah hasil kali antara gaya F dan lengan momennya. Torsi dilambangkan dengan lambang  .
.
 .
.
Satuan dari torsi adalah Nm (Newton meter).
Momen inersia adalah hasil kali partikel massa dengan kuadrat jarak tegak lurus partikel dari titik poros.

Satuan dari momen inersia adalah kg m²(Kilogram meter kuadrat).
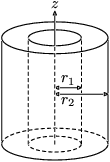
Besaran momen inersia dari beberapa benda.
Hubungan antara torsi dengan momen inersia
Hukum II Newton tentang rotasi
Keterangan:
- I : momen inersia (kg m²)
- α : percepatan sudut (rad/s²)
 : torsi (Nm)
: torsi (Nm)


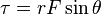





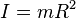
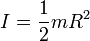




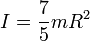


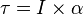
Tidak ada komentar:
Posting Komentar